Prof. Chen Avin

School of Electrical and
Computer Enginnering

Ben Gurion University
of the Negev

This work was supported by ISF grant number 1549/13: Structure, Dynamics and Algorithmics of Social Networks: An Axiom- Based Approach (Chen Avin, Zvi Lotker, David Peleg).

Core-Periphery in Networks: An Axiomatic Approach

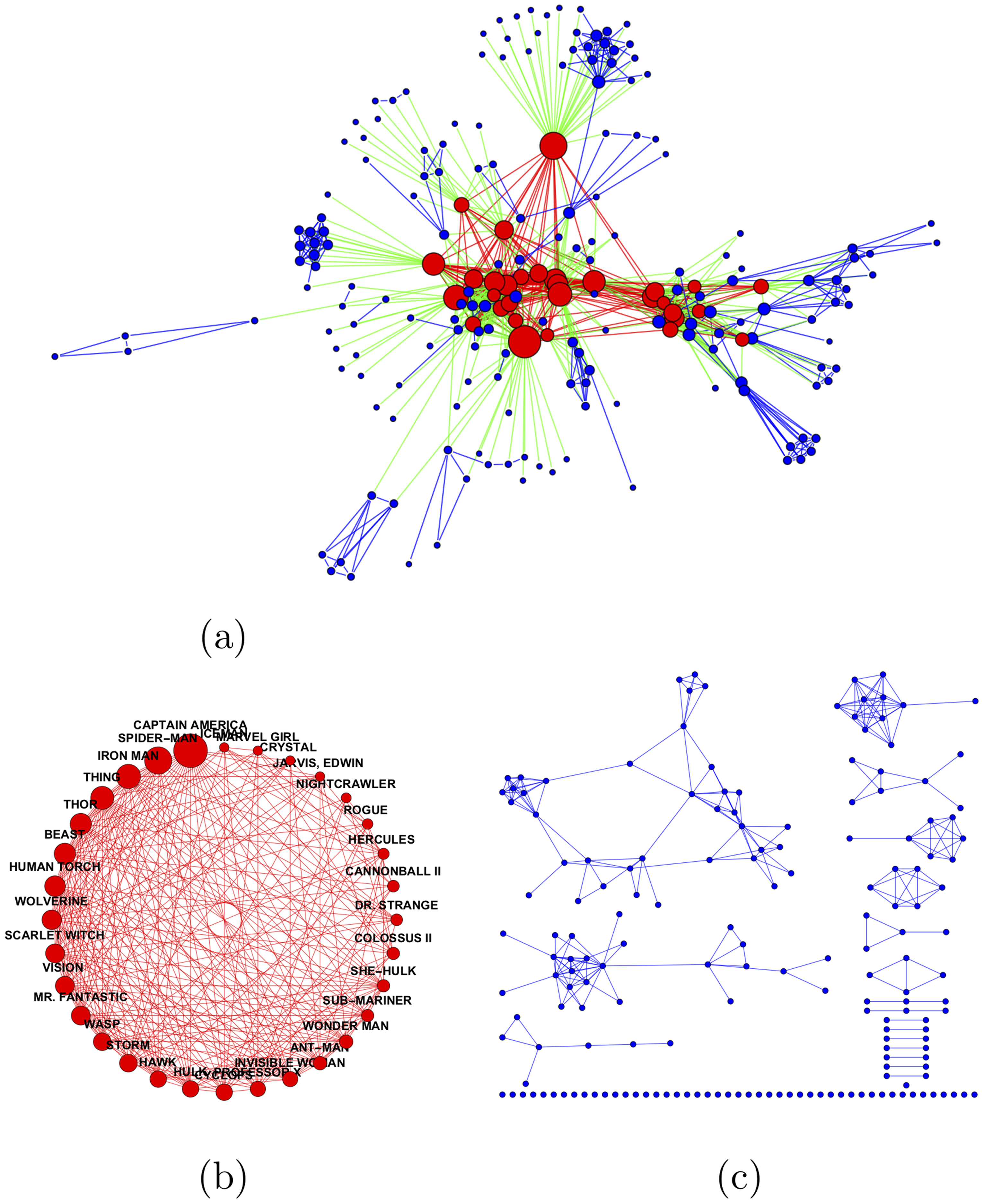plos Abstract: Recent evidence shows that in many societies worldwide the relative sizes of the economic and social elites are continuously shrinking. Is this a natural social phenomenon? What are the forces that shape this process? We try to address these questions by studying a Core-Periphery social structure composed of a social elite, namely, a relatively small but well-connected and highly influential group of powerful individuals, and the rest of society, the periphery. Herein, we present a novel axiom-based model for the forces governing the mutual influences between the elite and the periphery. Assuming a simple set of axioms, capturing the elite’s dominance, robustness, compactness and density, we are able to draw strong conclusions about the elite-periphery structure. In particular, we show that a balance of powers between elite and periphery and an elite size that is sub-linear in the network size are universal properties of elites in social networks that satisfy our axioms. We note that the latter is in controversy to the common belief that the elite size converges to a linear fraction of society (most recently claimed to be 1%). We accompany these findings with a large scale empirical study on about 100 real-world networks, which supports our results.

Publication: C. Avin, Z. Lotker, D. Peleg, Y.-A. Pignolet, and I. Turkel, “Elites in social networks: An axiomatic approach to power balance and price’s square root law,” PloS one, vol. 13, no. 10, p. e0205820, 2018.

Homophily and the Glass Ceiling Effect in Social Networks

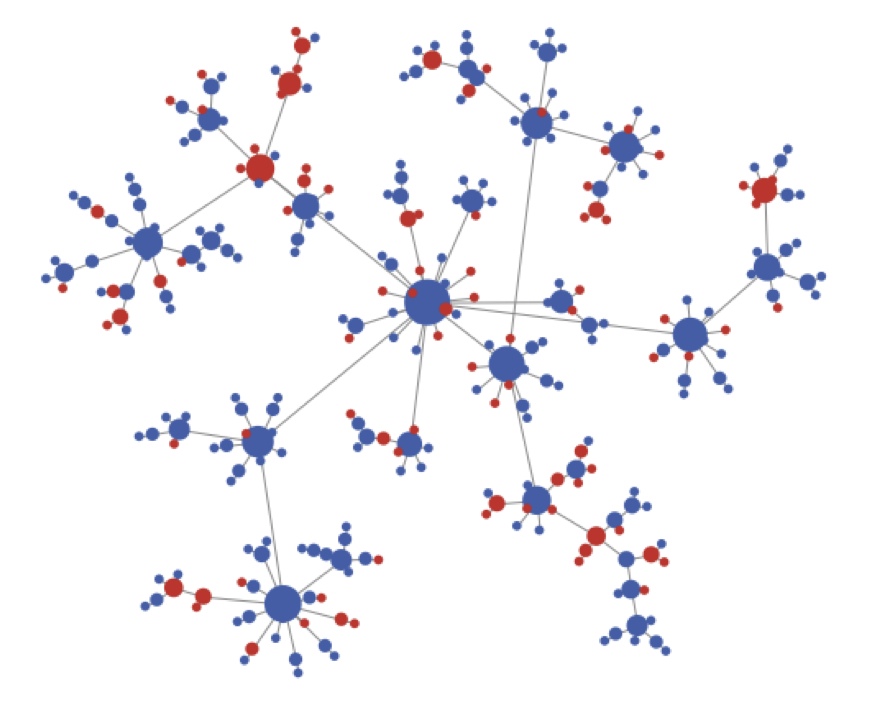Homophily Abstract: The glass ceiling effect has been defined in a recent US Federal Commission report as “the unseen, yet unbreakable barrier that keeps minorities and women from rising to the upper rungs of the corporate ladder, regardless of their qualifications or achievements”. It is well documented that many societies and organizations exhibit a glass ceiling. In this paper we formally define and study the glass ceiling effect in social networks and propose a natural mathematical model, called the biased preferential attachment model, that partially explains the causes of the glass ceiling effect. This model consists of a network composed of two types of vertices, representing two sub-populations, and accommodates three well known social phenomena: (i) the “rich get richer” mechanism, (ii) a minority-majority partition, and (iii) homophily. We prove that our model exhibits a strong moment glass ceiling effect and that all three conditions are necessary, i.e., removing any one of them will prevent the appearance of a glass ceiling effect. Additionally, we present empirical evidence taken from a mentor-student network of researchers (derived from the DBLP database) that exhibits both a glass ceiling effect and the above three phenomena.

Publication: C. Avin, B. Keller, Z. Lotker, C. Mathieu, D. Peleg, and Y.-A. Pignolet, “Homophily and the glass ceiling effect in social networks,” in Proceedings of the 2015 conference on innovations in theoretical computer science (ITCS), pp. 41–50, 2015.

Distributed Computing on Core-Periphery Networks: Axiom-based Design

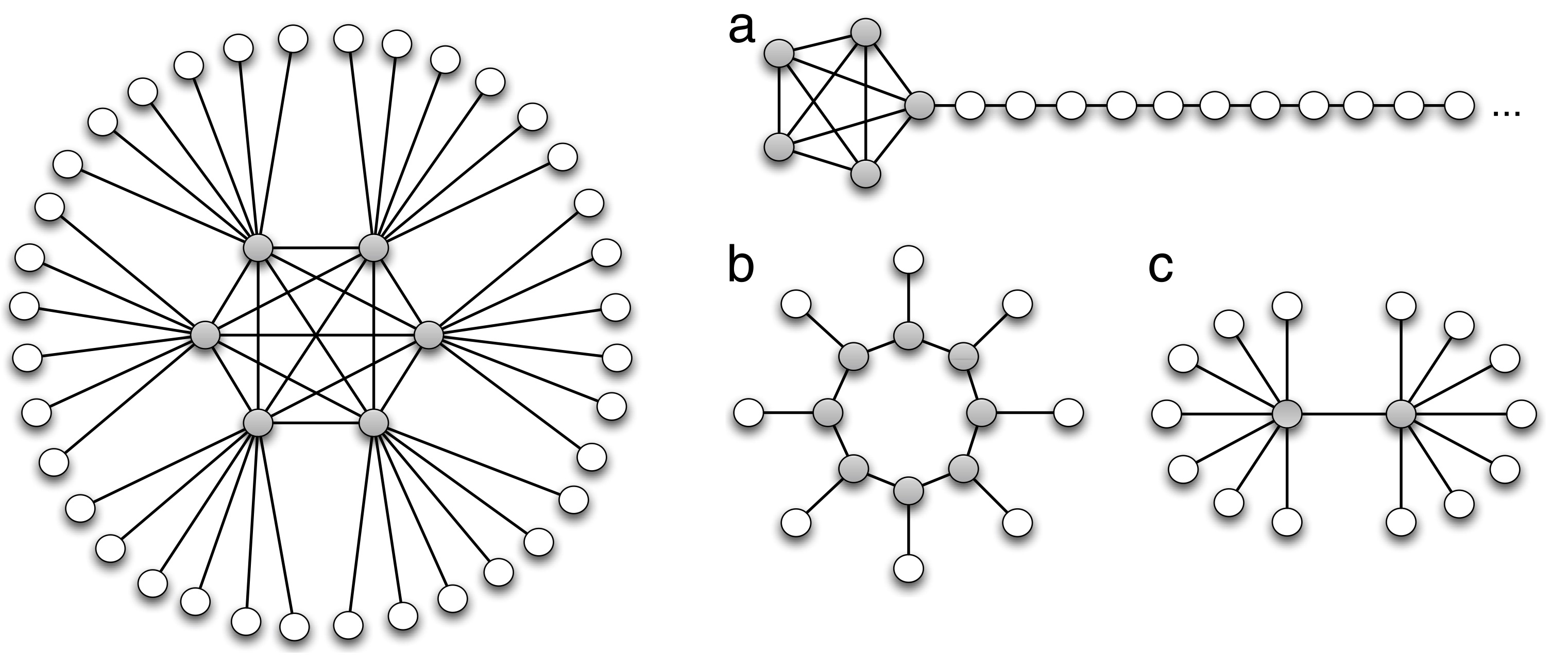Homophily Abstract: Inspired by social networks and complex systems, we propose a core-periphery network architecture that supports fast computation for many distributed algorithms and is robust and efficient in number of links. Rather than providing a concrete network model, we take an axiom-based design approach. We provide three intuitive (and independent) algorithmic axioms and prove that any network that satisfies all axioms enjoys an efficient algorithm for a range of tasks (e.g., MST, sparse matrix multiplication, etc.). We also show the minimality of our axiom set: for networks that satisfy any subset of the axioms, the same efficiency cannot be guaranteed for \emph{any} deterministic algorithm.

Publication: C. Avin, M. Borokhovich, Z. Lotker, and D. Peleg, “Distributed computing on core–periphery networks: Axiom-based design,” Journal of Parallel and Distributed Computing, vol. 99, pp. 51–67, 2017.

Preferential attachment as a unique equilibrium

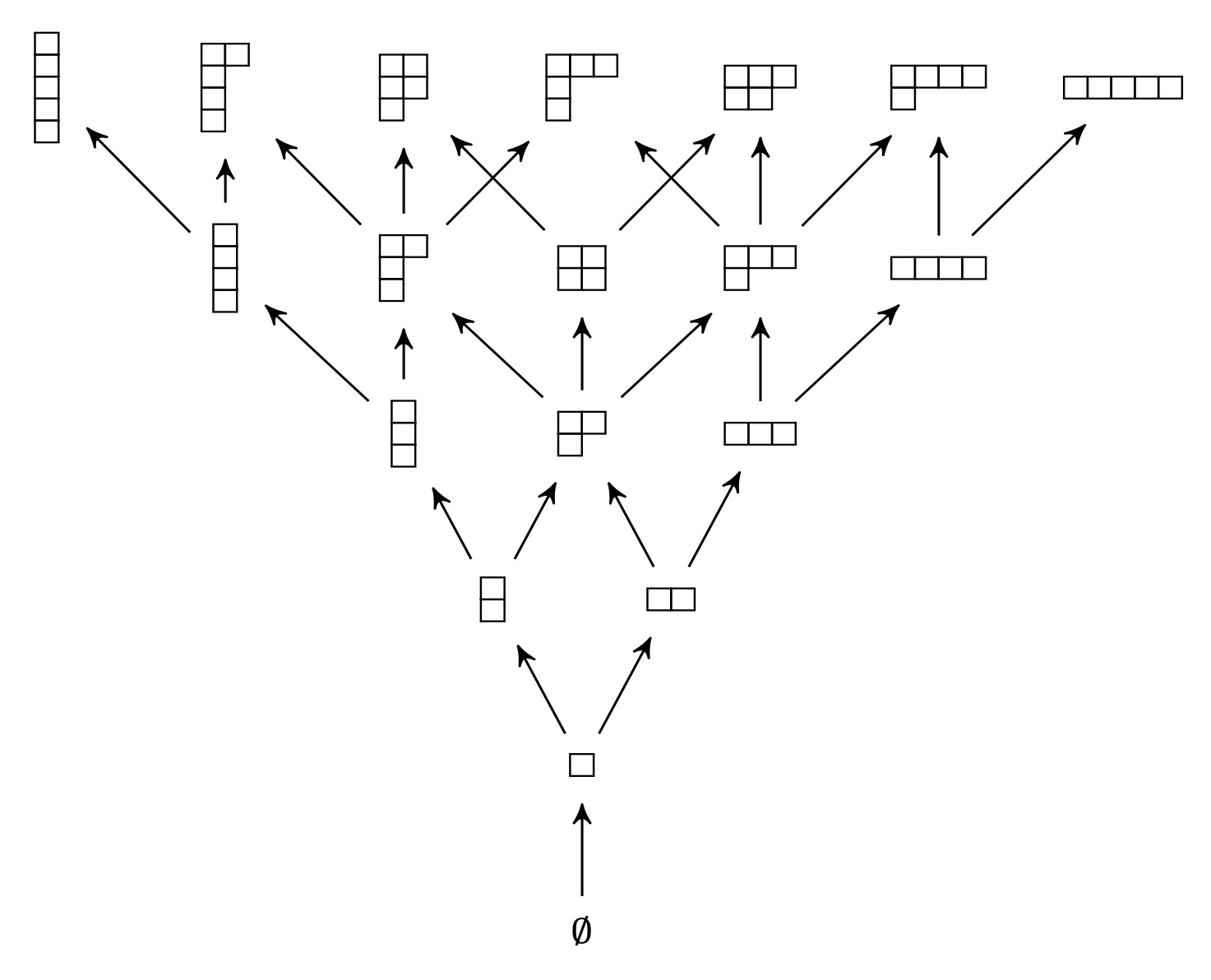Preferential Abstract: This paper demonstrates that the Preferential Attachment rule naturally emerges in the context of evolutionary network formation, as the unique Nash equilibrium of a simple social network game. In this game, each node aims at maximizing its degree in the future, representing its social capital in the “society” formed by the nodes and their connections. This result provides additional formal support to the commonly used Preferential Attachment model, initially designed to capture the “rich get richer” aphorism. In the process of establishing our result, we expose new connections between Preferential Attachment, random walks, and Young’s Lattice.

Publication: C. Avin, A. Cohen, P. Fraigniaud, Z. Lotker, and D. Peleg, “Preferential attachment as a unique equilibrium,” in Proceedings of the 2018 World Wide Web Conference (WWW), pp. 559–568, 2018.

Improved degree bounds and full spectrum power laws in preferential attachment networks

Enjoy the video :-)

Publication: C. Avin, Z. Lotker, Y. Nahum, and D. Peleg, “Improved degree bounds and full spectrum power laws in preferential attachment networks,” in Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), pp. 45–53, 2017. [C45]